Quelques notes pour répondre à certaines questions que la diffusion d'une image de M87 suscitent

Trous noirs et l’image de M87

Décrire proprement un trou noir demande à être fait dans le cadre de la relativité générale, la théorie qu’Einstein a développée en 1915 pour pallier aux inconsistances entre la finitude de la vitesse de la lumière et la gravitation de Newton. Si la mathématique n’est guère intuitive, le cheminement intellectuel peut s’énoncer avant de considérer les principales propriétés des trous noirs:

Einstein a décrit la gravitation au moyen d’une équation:

G_μν= 8ΠG T_μν

Le terme de gauche, G_μν, donne la géométrie de l’espace, celui de droite, 8ΠG T_μν, l’énergie et la masse contenue dans l’espace. Le terme de gauche, la géométrie, dicte la trajectoire d’une particule, ou un train par exemple; celui de droite contient toute les énergies en scène, il inclut donc l’énergie de la particule, ou celle du train. Le problème réside en ce que l’énergie de la particule ou du train change en fonction de sa trajectoire, en fonction donc de la géométrie, puisqu’elle détermine la trajectoire. Cette équation se mord la queue. On dit d’elle qu’elle est non linéaire.

Trouver des solutions à cette équation est extraordinairement difficile. Einstein l’a écrit à Max Born, un de ses amis, en ses termes (je cite de mémoire) : « Ach, wenn es nicht so schwierig wäre Lösungen zu finden ».

Un trou noir est une de ces solutions. Elle a été trouvée par Karl Schwarzschild en 1915 déjà, alors qu’il était un soldat allemand sur le front de l’Est. Il est mort l’année suivante.

Cette solution s’énonce :

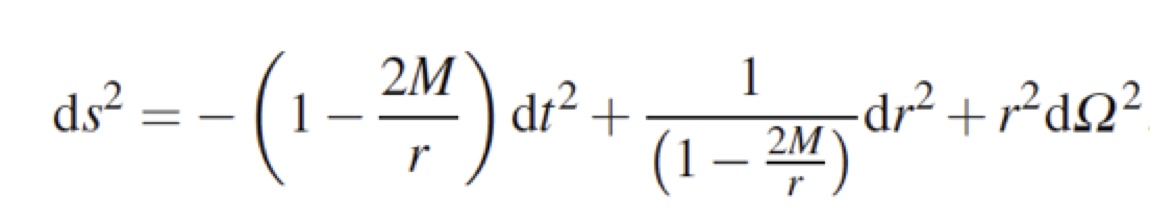
Il s’agit d’une prescription pour mesurer les distances dans l’espace dans lequel se trouve le trou noir. Cette prescription contient tout ce qui est nécessaire à la description d’un trou noir dont la masse est M.

Tout est peut-être donné par cette prescription, il n’empêche qu’il peut être bon de regarder un trou noir un peu différemment.

Pour s’échapper de la Terre jusqu’à l’infini il faut se donner une vitesse de départ de 11km/s (kilomètres par seconde) au moins. Si vous partez avec une vitesse plus petite, en sautant par exemple, vous retombez sur vos pieds. Si un objet est plus dense que la Terre cette vitesse est plus grande. Pour s’échapper d’une étoile de neutrons, une étoile extraordinairement dense, il faut une vitesse d’environ 100’000km/s. Si un objet est encore un peu plus dense, la vitesse nécessaire pour s’en échapper sera de 300’000km/s, la vitesse de la lumière. Comme une vitesse plus grande que celle de la lumière ne peut pas exister, rien, pas même la lumière ne peut s’en échapper. Un tel objet est noir, on dit de lui que c’est un trou noir, rien ne s’en échappe, pas même la lumière. Pour faire du Soleil un trou noir, il faudrait le comprimer jusqu’à ce que son diamètre soit de deux kilomètres. Il serait alors si dense que la lumière ne pourrait plus en sortir. L’équation ci-dessus décrit en mathématique cet état de fait. On appelle la surface sphérique d’un tel objet l’horizon, justement car on ne peut pas voir plus loin. Pour une masse comme celle du Soleil cette sphère aurait un rayon de 2 km.

Rien ne peut sortir du trou noir, mais il est parfaitement possible d’y entrer, d’où le nom de trou. Outre quelques distorsions pénibles, vous ne sentiriez rien en pénétrant dans un trou noir. L’horizon ne vous incommoderait pas particulièrement. Au fil de votre chute vers le trou noir et son horizon, vous pourriez donner de vos nouvelles à vos copains moins courageux et restés à distance respectable du trou noir jusqu’au moment où vous traversez l’horizon. Impossible après, puisque rien ne sort, donc pas vos nouvelles non plus, de faire savoir à l’extérieur si tout va bien. Les problèmes sérieux commencent lorsque vous arrivez près du centre. Là les forces qui vous déchirent deviennent infiniment grandes, vous êtes démembrés. Il y a là ce que l’on appelle une singularité. Une singularité que personne n’a jamais vue, car elle est pudiquement cachée par l’horizon. Les singularités nues n’existent pas, dit un théorème.

Comme rien ne sort d’un trou noir, l’image de M87 dont on parle beaucoup ces jours n’est pas celle du trou noir, mais celle de la matière lumineuse autour du trou noir lui-même. L’image n’est pas triviale dans ce sens que la présence du trou noir courbe les rayons lumineux de manière extrême. Toute masse défléchit les rayons lumineux à sa proximité. Le soleil courbe donc aussi les rayons lumineux qui passent proches de sa surface. L’effet est faible, mais mesuré depuis 1918, c’est une des prédiction de la relativité générale. La courbure des rayons lumineux augmente avec la densité de l’objet et devient telle que les rayons peuvent faire le tour de l’objet si celui ci est un trou noir. L’image dont on parle est donc l’image de la matière lumineuse autour du trou noir, déformée par la présence du trou noir très massif qui se trouve au centre de la galaxie M87.